Using Alloy, we can make an abstraction model of linked list. Linked list should have the following properties.
- It should have one header as a starting Node, it can link to another Node or null.
- Node has a link which can be another Node or null.
- There should be no cycle.
sig List and Node
The first an second property can be described with “sig”.
one sig List { header: lone Node }
The form of Alloy code looks like a class in OOP, but it’s actually a set. Alloy visually models the member as a label in the arrow, and List as a box.
List has a member named header which can be one of less than one (lone) Node member.
You can think header as a variable name, and Node as the type of the variable.
sig Node { link: lone Node }
Predicate
Then you can have a predicate that is true or false. You can use predicate for describing the acyclic property.
predicate looks like a method or function as it has parameters.
You can describe many ways to describe acyclic, one of them can be “all nodes should not be a link as null”.
And don’t forget about the header, so the link should start from header : link.header.*link
pred acyclic (l : List)
{
all n : l.header.*link | n !in n.^link
}
l.header.*link means l.header, l.header.link …
n.^link means n.link …
We check the predicate with “run acyclic” as if predicate is an entity to execute.


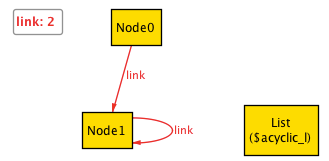
Alloy returns a list and two nodes that doesn’t have a cycle from the header, but it’s not what we expect.
We missed the fact that all the links from the header should be a Node (that is, has a link of Node or null)
fact
{
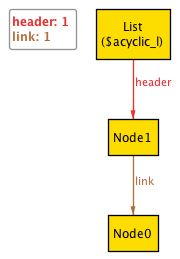
List.header.*link = Node
}
Now, we finally have what we expect.
Equivalence
You can describe the acyclic property in many forms, and you can prove the equivalence between them using Alloy.
pred acyclic2 (l : List)
{
no l.header or
some n: l.header.*link | no n.link // n.link is null
}
This predicate says that there can be a link without any element (base case), and some link from List.header.*link should have null. (induction case). Lone means zero or one, no means zero.
pred acyclic3 (l: List)
{
no (l.header).~link and
(all n: l.header.*link | lone n.~link)
}
~link means that something that refers link. It means that header’s link is not referenced, and all the links are referenced at most once.
You can run predicates, or you can assert the equivalence.
assert Equiv
{
all l : List | acyclic[l] <=> acyclic2[l]
}
check Equiv for 5
This command says check the assert with at most 5 elements.

Alloy transforms the code into SAT format, and runs the SAT solver to find a counter example, but it can’t find solution to this SAT problem, so it says they are equivalent.